02. 语音信号处理 Pycharm 实操——谱图
1. 目标
用 scipy.signal.stft 或 librosa.stft 画谱图(干净/带噪各一张)
2. 准备干净语料
准备干净的语音文件 clean.wav 放在合适的文件夹中。

3. 生成噪声语料并画出谱图
安装前一天没有安装,今天又需要的包:librosa 。
终端输入命令 pip install librosa 。
分析 GPT 给出的代码。
from pathlib import Path
import numpy as np
import librosa
import librosa.display
import soundfile as sf
import matplotlib.pyplot as plt
# ===== 路径设置 =====
ROOT = Path(__file__).resolve().parent
IN_WAV = ROOT / "clean.wav"
NOISY_WAV = ROOT / "noisy.wav"
FIG_CLEAN = ROOT / "spec_clean.png"
FIG_NOISY = ROOT / "spec_noisy.png"
if not IN_WAV.exists():
raise FileNotFoundError(f"找不到:{IN_WAV}(cwd={Path.cwd()})")Path(__file__).resolve().parent 表示 .py 文件所在的文件夹
好处:
让程序**以脚本所在文件夹为“基准点”**去找文件。
所以你不管:
用 PyCharm 跑
用 VS Code 跑
直接在 CMD / PowerShell 跑
甚至从别的目录跑
在终端里如果这样跑:
cd /d D:\document python speech_processing\speech_day2\make_noisy_and_specs.py- cwd = D:\document
- Day1 写法会去
D:\document\clean.wav找(当然找不到) - 脚本目录写法会去
D:\...\speech_day2\clean.wav找(能找到)
只要你的音频文件确实放在脚本同一个目录,一般就不会出现“因为运行目录不同导致找不到文件”。
与前一天代码对比:
# ====== 输入文件 ======
INPUT_WAV = "input.wav" # 输入音频的文件名
TARGET_SR = 16000 # 统一采样率到 16k
# ========================
out_dir = Path(".")
wav_in = Path(INPUT_WAV)Path("xxx.wav"):相对 cwd 当前工作路径,因此会到当前工作路径下找文件。
同理,输出文件位置 Path(".") 也是当前工作路径。
因此一旦当前工作路径和文件所在文件路径不匹配,则容易出现问题。
# ===== Step A:读取 clean,并统一采样率 =====
SR = 16000
y, sr = librosa.load(str(IN_WAV), sr=SR, mono=True)
print("Loaded:", IN_WAV, "len:", len(y), "sr:", sr)SR = 16000 : 先设定“目标采样率”为 16k。后面读入时会按这个来。
y, sr = librosa.load(str(IN_WAV), sr=SR, mono=True) :
这行做了三件事:
- 从 IN_WAV 读音频(IN_WAV 是文件路径)
mono=True:把音频变成单声道- 如果原来是双声道,librosa 会把左右声道做平均/合并
sr=SR:把音频重采样到 16k- 如果原来不是 16k(比如 44.1k),librosa 会自动 resample
- 如果原来就是 16k,它就不改
返回值:
y:一维 numpy 数组(波形,浮点数,通常范围在 [-1,1])sr:实际返回的采样率(因为你传了sr=16000,所以基本就是 16000)
print("Loaded:", IN_WAV, "len:", len(y), "sr:", sr) :
打印确认:读到了哪个文件、样本点数是多少、采样率是多少。 len(y) 是“采样点数”,如果想看“秒数”可以再算:len(y)/sr 。
# ===== Step B:按目标 SNR 加白噪声 =====
def add_white_noise_to_snr(clean: np.ndarray, snr_db: float, seed: int = 0):
rng = np.random.default_rng(seed)
noise = rng.standard_normal(size=clean.shape)
p_sig = np.mean(clean**2) + 1e-12
p_noise = np.mean(noise**2) + 1e-12
scale = np.sqrt(p_sig / (p_noise * (10 ** (snr_db / 10))))
noisy = clean + noise * scale
# 防削波:超过[-1,1]就整体缩放
peak = np.max(np.abs(noisy))
if peak > 0.99:
noisy = noisy / peak * 0.99 # 这里没有括号,实际上是 noisy × (0.99/peak)
return noisy.astype(np.float32)给 clean 波形加一段白噪声,并把噪声强度调到你指定的 SNR(比如 5 dB),然后把合成后的 noisy.wav 保存出来。
def add_white_noise_to_snr(clean: np.ndarray, snr_db: float, seed: int = 0): :
定义一个函数:输入干净语音 clean、目标 snr_db,输出带噪语音。
np.ndarray 指的是 NumPy 的数组类型(n-dimensional array,n 维数组)
seed 是随机种子:让你每次运行得到同一段噪声,方便复现实验。
1)seed 在代码里到底控制了什么?
rng = np.random.default_rng(seed) noise = rng.standard_normal(size=clean.shape)
default_rng(seed):用 seed 初始化一个随机数生成器standard_normal(...):从这个生成器里抽样,生成噪声所以 seed 直接决定了 noise 长什么样(哪一串随机数)。
2)常见 4 种使用场景
情况 A:固定 seed
目的:每次运行结果一致,方便你判断“代码改动带来的变化”。
做法:
seed = 0 # 固定改 STFT 参数/画图参数时,噪声不变,变化就只来自你的改动。
情况 B:要做“稳健结果”(论文实验更严谨)
目的:结果不依赖某一条噪声的“运气”,而是对多个随机噪声平均。
做法:跑多个 seed,取平均/方差:
seeds = [0, 1, 2, 3, 4] for s in seeds: noisy = add_white_noise_to_snr(clean, 5.0, seed=s) # 跑算法 -> 算指标 -> 记录最后汇报:平均提升多少 dB、标准差多少(哪怕只做 3 个 seed 也比 1 个强)。
情况 C:要“每次都生成不同 noisy”(不想重复)
目的:每次运行都想得到新的噪声样本。
做法 1:用时间相关的随机种子(最简单:不传 seed)
在 NumPy 里你可以让它自动用系统熵初始化:rng = np.random.default_rng() # 不给seed对应此处的函数,可以把 seed 默认值改成
None:def add_white_noise_to_snr(clean, snr_db, seed=None): rng = np.random.default_rng(seed)
seed=None→ 每次噪声都不一样(更“随机”)做法 2:手动换 seed(更可控)
比如用当前日期/实验编号:seed = 20251224情况 D:想“可复现 + 可追踪”(最像论文工程)
目的:既能生成不同 noisy,又能以后完全复现同一个 noisy。
做法:把 seed 写进文件名/日志:
noisy_snr5_seed0.wavnoisy_snr5_seed1.wav这样“这张图对应哪条 noisy”,就能立刻复现。
3)几个可能会踩的坑
坑 1:同 seed ≠ 同结果(如果改了 noise 的长度)
同一个 seed 生成的是“随机序列”,但你取多少个点会影响结果:
- 音频长度变了(更长/更短)
size=clean.shape就变了
→ 得到的噪声也会不同(因为截取的序列长度不一样)所以做“严格对比”时,输入长度最好固定。
坑 2:同 seed 在不同库/不同算法里不一定完全一致
现在用的是 NumPy 的
default_rng,它在 NumPy 内部是稳定的。
但如果你换成别的库的随机数(Pythonrandom、PyTorch、TF),seed 机制不通用。
rng = np.random.default_rng(seed) :
创建一个随机数生成器对象 rng。
default_rng 是 Numpy 推荐的新接口,比老的 np.random.seed() 更好用、更可控。
seed 一样 → 生成的随机序列就一样。
noise = rng.standard_normal(size=clean.shape) :
生成一段噪声数组 noise,长度和 clean 完全一致。
standard_normal 生成的是 高斯噪声:均值 0、标准差 1。
之所以叫“白噪声”:它的频谱在各频率上(理想情况下)平均分布,不偏向某个频段。
此时的 noise 强度是“默认的”,跟你的 clean 的强度没关系,所以还不能直接加。
p_sig = np.mean(clean**2) + 1e-12 :
这行在算干净语音的平均功率(power)。
clean**2:每个采样点平方(类似能量)
np.mean(...):对整段取平均,得到“每个采样点平均能量”,在信号处理中常用作功率估计。
- 1e-12:避免极端情况下 clean 全是 0 导致后面除 0。
你可以把 p_sig 理解成:这段语音整体有多“响”(更准确说是平均能量大小)。
p_noise = np.mean(noise**2) + 1e-12 :
同理,这行算的是刚生成的那段噪声的平均功率。
因为 noise 是标准高斯,理论上它功率大约接近 1,但实际会有波动,所以这里也算一下更稳。
我们知道了 “信号有多强” 和 “当前噪声有多强”
接下来关键问题:要把噪声乘多少倍,才能达到所需的 snr_db?
scale = np.sqrt(p_sig / (p_noise * (10 ** (snr_db / 10)))) :
算出噪声要乘多少倍,才能让加到 clean 上后的信噪比等于 snr_db(dB)
1)分贝的正式定义
对两个功率 的比值,分贝定义为:
这就是“对数单位 = 分贝”的来源:dB 就是这样定义出来的。
2)为什么定义里有 log?
因为很多实际系统(听觉、通信、放大器级联等)涉及的比值跨度很大。用对数有两个好处:
- 把很大的范围压缩:比值从 1 到 1,000,000,用 dB 变成 0 到 60
- 把乘法变加法:
两级增益相乘
在 dB 下变成
做系统分析很方便3)那为什么是 10,而不是别的?
这也是定义的一部分:历史上先有 “Bel(贝尔)”:
但 1 Bel 单位还是太大了,不好用,所以改用 十分之一 Bel,叫 deci-bel(分贝):
所以就变成了:
要注意:这里面的贝尔和分贝都是单位,单位大小变为原来的十分之一,那么数值就是原来的十倍(参考厘米和毫米)。
4)为什么有时是 20log?
因为此时比的不是功率,而是幅度/振幅(电压、声压、波形幅度等)。功率跟幅度的平方成正比:
代进去:
所以:
- 功率比 →
- 幅度比 →
Step 1: 先明确你想达到的目标
你希望最终满足:
把它变回线性比率:
令
那么目标噪声功率应该是:
现在手里有一段“原始噪声” noise
我们生成的 noise 是标准高斯白噪声,它自身有一个功率,但这个功率一般不是我们想要的,所以要缩放。
Step 2: 缩放噪声会怎么改变功率?
你把噪声乘一个系数 scale:
功率会变成:
Step 3: 让“缩放后的噪声功率”正好等于目标噪声功率
你要:
解出 scale:
把 换回 :
这就对应代码:
scale = np.sqrt(p_sig / (p_noise * (10 ** (snr_db / 10))))return noisy.astype(np.float32) :
把 noisy 这个 NumPy 数组转换成 float32 类型再返回。float32 每个数 4 字节,音频很长时,内存/写文件都更省。
TARGET_SNR_DB = 5.0 # 0更吵,10更干净
noisy = add_white_noise_to_snr(y, TARGET_SNR_DB, seed=0)
sf.write(str(NOISY_WAV), noisy, SR)
print("Saved:", NOISY_WAV)刚才的函数实例化,带入需要的信噪比 5dB 。y 是干净语音的信号数组。
sf.write(str(NOISY_WAV), noisy, SR) 将函数返回的加过噪声的语音数组存储下来。三个参数分别为:文件路径, 数据, 采样率。
# ===== Step C:STFT -> dB(两张图统一参考,保证可比)===== 这里自己按照逻辑调整了顺序
WINDOW = "hann"
WIN_LENGTH = 400 # 25ms @ 16k
HOP_LENGTH = 160 # 10ms @ 16k
N_FFT = 512
def stft_mag(x):
D = librosa.stft(x, n_fft=N_FFT, hop_length=HOP_LENGTH,
win_length=WIN_LENGTH, window=WINDOW)
return np.abs(D)
S_clean = stft_mag(y)
S_noisy = stft_mag(noisy)Step C 做的事可以概括成一句话:把时域波形变成“随时间变化的频谱”(STFT),然后取幅度得到谱图的原材料。
WINDOW(窗函数)
"hann":把每帧边缘逐渐压小,减少频谱泄漏- 语音任务里 Hann 是默认常用选择。
每帧其实是在“截取一小段信号”。直接硬截会在两端突然断开,相当于乘了一个“矩形窗”,会导致频谱泄漏更明显。
Hann 窗做的事:把帧的两端缓慢压到 0,让截断更平滑 → 泄漏更小 → 谱图更干净。
WIN_LENGTH(窗长 / 每一帧取多长)
WIN_LENGTH=400:每帧取 400 个采样点- 采样率 16k 时:400/16000 = 0.025s = 25ms
- 25ms 是语音谱图常用帧长:能看到谐波结构,也不会太糊。
HOP_LENGTH(帧移 / 两帧之间隔多少点)
HOP_LENGTH=160:相邻两帧起点相隔 160 个点- 160/16000 = 10ms
- 也很常用:时间分辨率够,谱图不会太稀。
FFT 点数 N_FFT(每帧用多少点来算频谱)
N_FFT = 512 的意思是:每一帧做 STFT 时,用 512 点 FFT 来把这一帧从时域变到频域。它主要带来三件事:
1)它决定“频率格子(bin)有多少”和“每格多宽”
采样率 SR=16000 时:
- 频率间隔
意思是:相邻两个频率 bin 的中心频率差 31.25 Hz。
- 非负频率 bin 数(音频是实数,通常只留 0~SR/2,负频率部分与正频率是镜像的,信息是重复的)
所以你的谱图矩阵在频率方向通常是 257 行,有256个间隔。
2)它决定谱图频率轴的“最高频”
最高频是 Nyquist:
所以谱图频率范围是 0~8000Hz(这对 16k 语音足够了)。
3)为什么常用 512(这套参数下的原因)
现在 WIN_LENGTH=400(25ms)。FFT 点数一般取:
- 不小于窗长(否则信息会被截断/不合理)
- 常取 2 的幂(FFT 计算更高效、也更常用)
400 不是 2 的幂,最近的 ≥400 的 2 的幂就是 512。
所以设 N_FFT=512 等价于:每帧先用 400 点窗取出有效数据,再补零到 512 点做 FFT。
补零:让频率轴网格更密、谱图更平滑(但不会凭空增加真正的分辨能力)。
把每帧长度不够的部分用 0 填满,让 FFT 计算用固定的 512 点长度。
具体到这组参数:
- 每帧真正取出来的是
WIN_LENGTH=400个点(25ms)- 但让 FFT 用
N_FFT=512点来算所以库会做一件事:
把这 400 个点后面再接上 112 个 0,变成 512 点,然后对这 512 点做 FFT
用符号写就是:
为什么要补零?
1)让频率轴更“细”(bin 更密)
频率间隔是:
- 用 400 点做 FFT: Hz
- 用 512 点做 FFT: Hz
所以补零后,你的频率格子更密,谱图看起来更平滑、更像“高分辨率的网格”。
2)计算更方便/更快(2 的幂 FFT)
512 是 ,FFT 算法对 2 的幂长度通常更高效、实现也更成熟。
重要:补零不会“凭空增加信息”
补零只是让频谱在频率轴上插值更密,看起来更平滑;
真正能分辨多细的频率细节,主要还是由窗长 400 点决定的。可以把它类比成:
- 窗长 400:你用 25ms 的“观察时间”
- N_FFT 512:你把频率坐标尺刻得更细,但观察时间没变
补零 = 把频谱“画得更细”,不是“听得更细”。
def stft_mag(x):
D = librosa.stft(x, n_fft=N_FFT, hop_length=HOP_LENGTH,
win_length=WIN_LENGTH, window=WINDOW)
return np.abs(D)D 是 复数矩阵(complex)
形状:
- 行:
N_FFT/2 + 1(因为输入是实数,只保留非负频率) - 列:由音频长度和 hop 决定的帧数
np.abs(D) 为什么是谱图?
D 每个元素是复数:
复数包含两部分信息:
- 幅度(强度):
- 相位(角度):
np.abs(D) 就是在做:
这就是谱图最常画的东西:能量/强度随时间和频率的分布。
S_clean = stft_mag(y)
S_noisy = stft_mag(noisy)将干净和噪声的谱图实例化。
# 关键:两张图用同一个 ref(用 clean 的最大值)
ref = np.max(S_clean) + 1e-12
S_clean_db = librosa.amplitude_to_db(S_clean, ref=ref)
S_noisy_db = librosa.amplitude_to_db(S_noisy, ref=ref)这段代码是在把“线性幅度谱”转换成 dB(对数刻度),并且确保 clean 和 noisy 两张图用同一把尺子,这样颜色深浅才可直接比较。
ref = np.max(S_clean) + 1e-12 :
S_clean是 clean 的幅度谱矩阵(都是非负数)。np.max(S_clean)取的是 clean 全部时频点里最大的幅度。+ 1e-12是为了防止极端情况 ref=0(避免除 0 或 log(0))。
所以 ref 就是一个标尺:把 clean 的最大幅度当作 0 dB 的基准。
librosa.amplitude_to_db(S, ref=ref) 在算什么?
它做的本质是:
所以:
- 当
S == ref时: dB
→ 最大幅度点是 0 dB - 当
S比ref小 10 倍:
dB - 小 100 倍:-40 dB
- 小 1000 倍:-60 dB
这就是为什么谱图常用 dB:能把很大的动态范围压缩,细节更容易看见。
优化小建议(更稳、更“论文范”)
有时 clean 的最大值可能是某个瞬时尖峰,导致整体都偏暗。更稳的做法是用百分位数做 ref:
ref = np.percentile(S_clean, 99.9) + 1e-12取 S_clean 里99.9% 分位数对应的值,这样 0 dB 对应“接近最大但不被极端点支配”的能量,更好看、更稳定。
VMIN, VMAX = -80, 0
plt.figure() # 新建一张空画布(一个 figure)
librosa.display.specshow(S_clean_db, sr=SR, hop_length=HOP_LENGTH,
x_axis="time", y_axis="linear", vmin=VMIN, vmax=VMAX)
plt.colorbar(format="%+2.0f dB")
plt.title("CLEAN Spectrogram")
plt.tight_layout()
plt.savefig(str(FIG_CLEAN), dpi=200)
plt.close()
print("Saved:", FIG_CLEAN)
plt.figure()
librosa.display.specshow(S_noisy_db, sr=SR, hop_length=HOP_LENGTH,
x_axis="time", y_axis="linear", vmin=VMIN, vmax=VMAX)
plt.colorbar(format="%+2.0f dB")
plt.title(f"NOISY Spectrogram (SNR={TARGET_SNR_DB} dB)")
plt.tight_layout()
plt.savefig(str(FIG_NOISY), dpi=200)
plt.close()
print("Saved:", FIG_NOISY)后面画谱图一般会写(无论是 specshow 还是 imshow):
librosa.display.specshow(S_db, vmin=VMIN, vmax=VMAX)vmax=0:把 0 dB 显示成最亮/最热的颜色vmin=-80:把 -80 dB 以及更低的部分都压到最暗(当成背景)
超过
vmax的值会“饱和为最亮”,低于vmin的值会“饱和为最暗”。
VMIN决定你想显示到“多弱的能量”:
- VMIN 越小(更负,如 -90)
→ 把更弱的东西也显示出来
→ 细节更多,但背景/噪声也更容易“脏、雾”- VMIN 越大(不那么负,如 -60)
→ 把弱能量直接压黑
→ 背景更干净、对比更强,但会丢掉一些弱细节一般经验:
- -60 ~ 0:更突出主要结构(适合论文图、清晰)
- -80 ~ 0:更全面(能看到更多弱能量)
- -100 ~ 0:适合看非常弱的背景,但容易显得“雾蒙蒙”
plt.colorbar(format="%+2.0f dB") :
加一个颜色条,并用 dB 的格式显示刻度(比如 -80、-60、-40、-20、0)。
plt.tight_layout()
自动调整边距,避免标题/坐标轴/色条挤在一起或被裁掉。
plt.savefig(str(FIG_CLEAN), dpi=200)
把当前这张图保存成文件:
FIG_CLEAN 是输出路径(比如 spec_clean.png)
dpi=200 表示清晰度(论文一般 200–300 都可以)
plt.close()
关闭这张图,释放内存(脚本批量画图时很重要,否则会越占越多内存)。
完整代码:
调整了 vmin 到 -60
from pathlib import Path
import numpy as np
import librosa
import librosa.display
import soundfile as sf
import matplotlib.pyplot as plt
# ===== 路径设置 =====
ROOT = Path(__file__).resolve().parent
IN_WAV = ROOT / "clean.wav"
NOISY_WAV = ROOT / "noisy.wav"
FIG_CLEAN = ROOT / "spec_clean.png"
FIG_NOISY = ROOT / "spec_noisy.png"
if not IN_WAV.exists():
raise FileNotFoundError(f"找不到:{IN_WAV}(cwd={Path.cwd()})")
# ===== Step A:读取 clean,并统一采样率 =====
SR = 16000
y, sr = librosa.load(str(IN_WAV), sr=SR, mono=True)
print("Loaded:", IN_WAV, "len:", len(y), "sr:", sr)
# ===== Step B:按目标 SNR 加白噪声 =====
def add_white_noise_to_snr(clean: np.ndarray, snr_db: float, seed: int = 0):
rng = np.random.default_rng(seed)
noise = rng.standard_normal(size=clean.shape)
p_sig = np.mean(clean**2) + 1e-12
p_noise = np.mean(noise**2) + 1e-12
scale = np.sqrt(p_sig / (p_noise * (10 ** (snr_db / 10))))
noisy = clean + noise * scale
# 防削波:超过[-1,1]就整体缩放
peak = np.max(np.abs(noisy))
if peak > 0.99:
noisy = noisy / peak * 0.99
return noisy.astype(np.float32)
TARGET_SNR_DB = 5.0 # 0更吵,10更干净
noisy = add_white_noise_to_snr(y, TARGET_SNR_DB, seed=0)
sf.write(str(NOISY_WAV), noisy, SR)
print("Saved:", NOISY_WAV)
# ===== Step C:STFT -> dB(两张图统一参考,保证可比)=====
WINDOW = "hann"
WIN_LENGTH = 400 # 25ms @ 16k
HOP_LENGTH = 160 # 10ms @ 16k
N_FFT = 512
def stft_mag(x):
D = librosa.stft(x, n_fft=N_FFT, hop_length=HOP_LENGTH,
win_length=WIN_LENGTH, window=WINDOW)
return np.abs(D)
S_clean = stft_mag(y)
S_noisy = stft_mag(noisy)
# 关键:两张图用同一个 ref(用 clean 的最大值)
ref = np.percentile(S_clean, 99.9) + 1e-12
S_clean_db = librosa.amplitude_to_db(S_clean, ref=ref)
S_noisy_db = librosa.amplitude_to_db(S_noisy, ref=ref)
VMIN, VMAX = -60, 0
plt.figure() # 新建一张空画布(一个 figure)
librosa.display.specshow(S_clean_db, sr=SR, hop_length=HOP_LENGTH,
x_axis="time", y_axis="linear", vmin=VMIN, vmax=VMAX)
plt.colorbar(format="%+2.0f dB")
plt.title("CLEAN Spectrogram")
plt.tight_layout()
plt.savefig(str(FIG_CLEAN), dpi=200)
plt.close()
print("Saved:", FIG_CLEAN)
plt.figure()
librosa.display.specshow(S_noisy_db, sr=SR, hop_length=HOP_LENGTH,
x_axis="time", y_axis="linear", vmin=VMIN, vmax=VMAX)
plt.colorbar(format="%+2.0f dB")
plt.title(f"NOISY Spectrogram (SNR={TARGET_SNR_DB} dB)")
plt.tight_layout()
plt.savefig(str(FIG_NOISY), dpi=200)
plt.close()
print("Saved:", FIG_NOISY)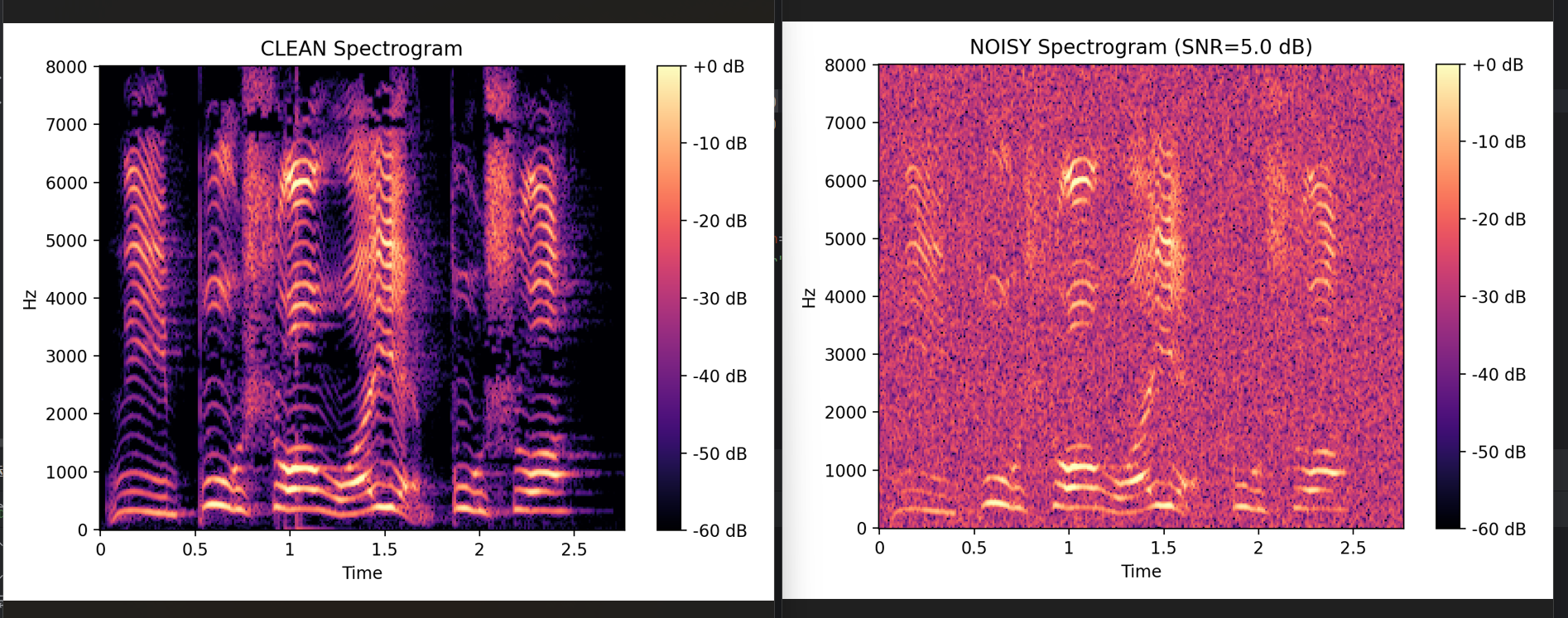
更新日志
1145e-于6e643-于
